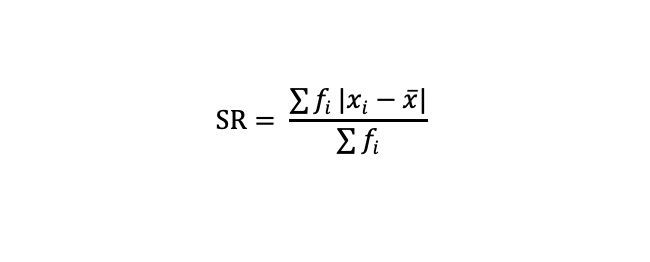
Dalam dunia yang penuh dengan data dan informasi, kemampuan untuk memahami dan menganalisis variasi dalam kumpulan angka menjadi semakin penting.
Salah satu alat yang sangat berguna untuk tujuan ini adalah simpangan rata-rata. Mari kita jelajahi rumus, cara pengerjaan, dan aplikasi praktis dari konsep statistik yang menarik ini.
Simpangan rata-rata, atau mean absolute deviation (MAD) dalam bahasa Inggris, dihitung dengan rumus berikut:
MAD = Σ|x – μ| / n
Di mana:
– Σ adalah simbol penjumlahan
– |x – μ| adalah nilai absolut dari selisih antara setiap nilai data (x) dan rata-rata (μ)
– n adalah jumlah data
Cara Pengerjaan
Langkah-langkah untuk menghitung simpangan rata-rata adalah sebagai berikut:
- Hitung rata-rata (mean) dari seluruh data.
- Untuk setiap nilai data, hitung selisihnya dari rata-rata.
- Ambil nilai absolut dari selisih tersebut (hilangkan tanda negatif jika ada).
- Jumlahkan semua nilai absolut tersebut.
- Bagi hasil penjumlahan dengan jumlah data.
Contoh Soal dan Jawaban
Mari kita lihat beberapa contoh penggunaan simpangan rata-rata dalam konteks kehidupan sehari-hari.
Contoh 1: Waktu Perjalanan ke Kantor
Soal:
Andi mencatat waktu perjalanannya ke kantor selama 5 hari kerja (dalam menit): 25, 30, 28, 35, 27. Hitunglah simpangan rata-rata waktu perjalanan Andi.
Jawaban:
- Hitung rata-rata: (25 + 30 + 28 + 35 + 27) / 5 = 29 menit
- Hitung selisih dari rata-rata:
25 – 29 = -4
30 – 29 = 1
28 – 29 = -1
35 – 29 = 6
27 – 29 = -2
- Ambil nilai absolut:
|-4| = 4, |1| = 1, |-1| = 1, |6| = 6, |-2| = 2
- Jumlahkan nilai absolut: 4 + 1 + 1 + 6 + 2 = 14
- Bagi dengan jumlah data: 14 / 5 = 2,8
Jadi, simpangan rata-rata waktu perjalanan Andi adalah 2,8 menit.
Interpretasi: Rata-rata, waktu perjalanan Andi menyimpang sekitar 2,8 menit dari rata-rata 29 menit.
Contoh 2: Pengeluaran Bulanan
Soal:
Budi mencatat pengeluaran hariannya selama seminggu (dalam ribuan rupiah): 50, 75, 60, 80, 55, 90, 70. Hitunglah simpangan rata-rata pengeluaran Budi.
Jawaban:
- Hitung rata-rata: (50 + 75 + 60 + 80 + 55 + 90 + 70) / 7 = 68,57
- Hitung selisih dari rata-rata:
50 – 68,57 = -18,57
75 – 68,57 = 6,43
60 – 68,57 = -8,57
80 – 68,57 = 11,43
55 – 68,57 = -13,57
90 – 68,57 = 21,43
70 – 68,57 = 1,43
- Ambil nilai absolut dari selisih
- Jumlahkan nilai absolut: 18,57 + 6,43 + 8,57 + 11,43 + 13,57 + 21,43 + 1,43 = 81,43
- Bagi dengan jumlah data: 81,43 / 7 = 11,63
Jadi, simpangan rata-rata pengeluaran Budi adalah 11,63 ribu rupiah.
Interpretasi: Rata-rata, pengeluaran harian Budi menyimpang sekitar Rp 11.630 dari rata-rata Rp 68.570.
Kegunaan Rumus Simpangan Rata-rata
Simpangan rata-rata memiliki beberapa kegunaan penting:
- Mengukur Variabilitas: Simpangan rata-rata memberikan gambaran tentang seberapa tersebar data dari nilai rata-ratanya. Semakin besar simpangan rata-rata, semakin besar variasi dalam data.
- Mengidentifikasi Konsistensi: Dalam contoh waktu perjalanan Andi, simpangan rata-rata yang kecil menunjukkan bahwa waktu perjalanannya cukup konsisten dari hari ke hari.
- Analisis Risiko: Dalam konteks keuangan, simpangan rata-rata dapat digunakan untuk mengukur volatilitas investasi atau fluktuasi pengeluaran, seperti pada contoh pengeluaran Budi.
- Kontrol Kualitas: Dalam industri manufaktur, simpangan rata-rata dapat digunakan untuk mengukur konsistensi produk dan mengidentifikasi proses yang mungkin memerlukan perbaikan.
- Perbandingan Dataset: Simpangan rata-rata memungkinkan kita membandingkan variabilitas antara dataset yang berbeda, bahkan jika rata-ratanya berbeda.
- Evaluasi Performa: Dalam olahraga atau pendidikan, simpangan rata-rata dapat digunakan untuk menilai konsistensi performa atlet atau siswa.
- Peramalan: Dalam analisis tren, simpangan rata-rata dapat membantu dalam memahami seberapa akurat peramalan atau prediksi.
- Deteksi Outlier: Nilai-nilai yang jauh melebihi simpangan rata-rata mungkin merupakan outlier yang memerlukan investigasi lebih lanjut.
Dalam kehidupan sehari-hari, pemahaman tentang simpangan rata-rata dapat membantu kita membuat keputusan yang lebih baik. Misalnya, seorang manajer proyek dapat menggunakan simpangan rata-rata untuk menilai reliabilitas estimasi waktu penyelesaian tugas.
Seorang investor dapat menggunakannya untuk membandingkan risiko relatif dari berbagai opsi investasi. Bahkan dalam konteks personal, kita dapat menggunakan simpangan rata-rata untuk menganalisis dan memperbaiki kebiasaan kita, seperti pola tidur atau pola makan.